Sectur da download

Infurmaziun davart il download

En il sectur da download pudais Vus chargiar giu ils documents dal Plan d'instrucziun sco PDF per als stampar.

MA.1

Dumber e variabla

A

Operar e numnar

4

Las scolaras ed ils scolars san cumparegliar e transfurmar terms, schliar equaziuns, applitgar leschas e reglas.

renviaments

AS

MA.1.A.4

Las scolaras ed ils scolars ...

1

a

  • san accordar differentas quantitads ina a l'autra (p.ex. 8 e 4 buttuns → 6 e 6 buttuns).

 

b

  • san decumponer en differentas modas dumbers fin 20 (p.ex. 5 = 1 + 4 = 3 + 2 = 3 + 1 + 1) e transfurmar quels (lescha da commutativitad: p.ex. 5 + 3 = 3 + 5).

 

c

  • san utilisar l'adiziun sco operaziun inversa da la subtracziun (p.ex. 18 - 15 = 3, perquai che 15 + 3 = 18).
  • san trair a niz relaziuns tranter adiziuns cun la lescha da commutativitad (p.ex. 2 + 18 = 18 + 2) e la lescha d'associativitad (p.ex. 17 + 18 = 17 + 3 + 15 = 20 + 15).

 

d

  • san trair a niz relaziuns tranter products (p.ex. 6 · 8 è per 8 pli grond che 5 · 8 u cun la lescha da commutativitad: p.ex. 8 · 3 = 3 · 8).

 

2

e

  • chapeschan la divisiun sco operaziun inversa da la multiplicaziun ed il connex cun l'adiziun (p.ex. 28 : 7 = 4 → 28 = 4 · 7 → 28 = 7 + 7 + 7 + 7).
  • san trair a niz relaziuns tranter il pitschen amulain e l'amulain da diesch.

 

f

  • san transfurmar products cun dublar e smesar (p.ex. 8 · 26 = 4 · 52 = 2 · 104).
  • san trair a niz la lescha d'associativitad en connex cun summas e products (p.ex. 136 + 58 + 42 = 136 + (58 + 42); 38 · 4 · 25 = 38 · (4 · 25)).
  • san arrundar dumbers natirals sin dumbers da 10, da 100 e da 1'000.

 

orientierungspunkt

g

  • san identifitgar dumbers divisibels cun 2, 5, 10, 100, 1'000.
  • san arrundar dumbers decimals (p.ex. 17'456 sin in dumber da 100; 1.745 sin in dieschavel).

 

h

  • san schliar equaziuns cun variablas cun inserir dumbers u cun operaziuns inversas.
  • san observar las reglas da quint punct avant stritg e las reglas da parantesa
    (p.ex. 4 + 8 - 2 · 3 = 6; (4 + 8 - 2) · 3 = 30; 4 + (8 - 2) · 3 = 22).
  • amplificaziun: san trair a niz reglas da divisiun cun 3, 4, 6, 8, 9, 25, 50 ed identifitgar ils divisurs da dumbers natirals.

 

3

i

  • san scriver in product cun medems facturs sco potenza e viceversa (p.ex. 15 · 15 · 15 = 15³ ; a · a · a · a = a⁴).
  • san applitgar la lescha da distributivitad tar la transfurmaziun da terms (p.ex. (b + c) = a · b + a · c = ab + ac).
  • san arrundar resultats a moda raschunaivla.
  • amplificaziun: chapeschan las convenziuns davart la notaziun da terms algebraics (p.ex. abc = a · b · c aber 789 ≠ 7 · 8 · 9).

 

j

  • amplificaziun: san schliar equaziuns linearas cun ina variabla cun agid da transfurmaziuns d'equivalenza (p.ex. 5x + 3 = 7).
  • amplificaziun: san adir e subtrahar polinoms (p.ex. 3(a² + 2b) - 2(a² + b) = a² + 4b).
  • amplificaziun: san multiplitgar e schliar parantesas en terms (decumposiziun en facturs).
  • amplificaziun: san explitgar equaziuns cun pleds (p.ex. x = y + 1 → x è per 1 pli grond che y) e transponer equaziuns da text en terms.
  • amplificaziun: san transfurmar resp. simplifitgar a moda utila terms cun variablas (schliar parantesas, multiplitgar, scursanir ed applitgar las reglas da segn positiv e negativ).

 

orientierungspunkt

k

  • san adir e subtrahar terms cun variablas (p.ex. a + 2a + b + 3b + ¼ + ⅜ = 3a + 4b + ⅝).

 

l

  • san schliar equaziuns quadratas cun agid da la decumposiziun en facturs (p.ex. x² - 4 = 0).
  • san transfurmar e calcular terms cun potenzas e ragischs quadratas
    (p.ex. ).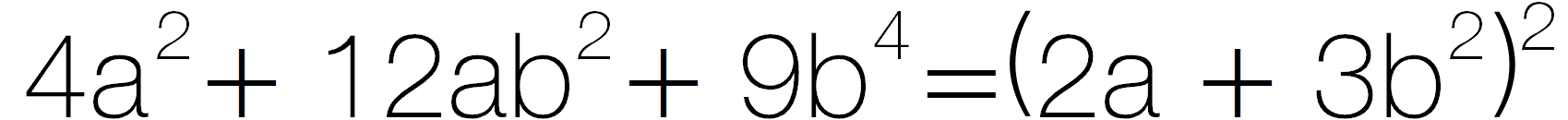
  • san applitgar las reglas da quint 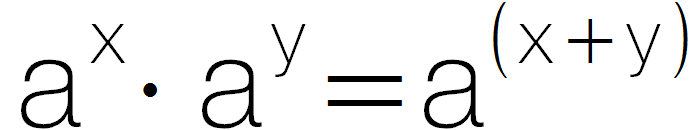e la regla potenza avant punct avant stritg.

 

m

  • san transfurmar terms fracziunals cun binoms.
  • san observar leschas da quint tar terms cun potenzas e ragischs sco era tar dumbers en scripziun scientifica.
  • san schliar equaziuns da fracziuns cun in dumber nunenconuschent en il numnader (p.ex.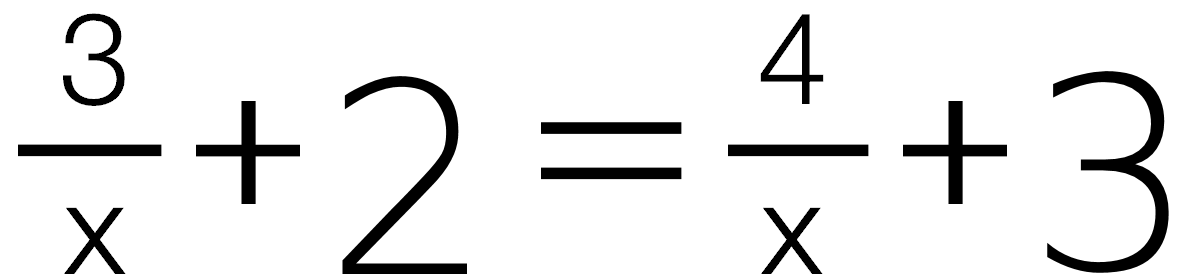) ed equaziuns cun in parameter (p.ex. ax + a = 7).
  • san schliar sistems d'equaziuns linearas cun 2 dumbers nunenconuschents.